Construct the two-state Hamiltonian

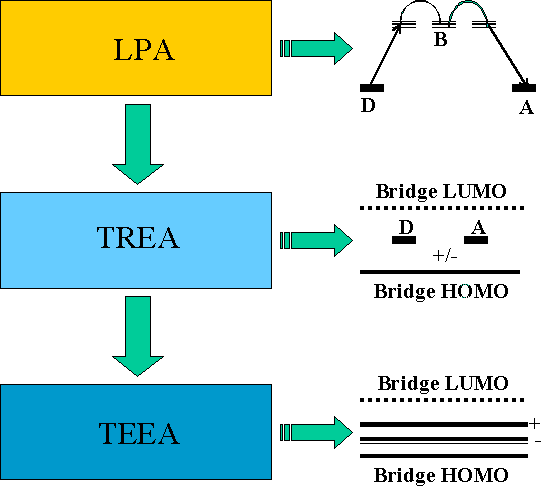
The three levels of the effective two-state approximation.

The reason that the LPA doesn't work is obvious. Because the time Green functions is the integration of the Schroedinger equation of motion therefore a time cumulative, the LPA result will certainly disagree more and more with the exact ones as the propogation goes, since the perturbative results always have more or less deviations from the exact ones that will sooner or later have amplified influence to an important amount in a time cumulative no matter how small it might have been. In my opinion, changing E_tunneling to get a series of T_DA that could reproduce the exact propogation is theoretically not right, because it is theoretically right to have higher order deviations.

Code: LPA:

Propogate a two-state system

A signal processing point of view of the two-state approximation

The process of constructing a TSA which is valid for describing the electronic dynamics of a system with large dimension resembles retrieving a signal from a background of noise. In our theory, the interested 'signal' is the superexchange part of electron current (or the tunneling current), the 'noise' is the transport-like part which inevitably arises from the multisite hopping.

The question is, does the TSA thus constructed continue to be legitimate when the 'signal' gets weaker and weaker than the 'noise'? We know that in weak coupling cases, it is the weak one of the D and A characters that plays the decisive role on deriving the TSA. Suppose, in an extreme case, that the contributions from the 'heat bath', namely, the wave function scatterings from the bridge sites to the D and A states, constitute 99% of the whole character, do we believe that we would still be able to restore the 1% 'signal' from such a noisy background?

Perhaps yes. But an ensemble average point of view must enter our sight.

Perhaps no. Because the 'signal' is simply too weak to be restored.